The Iterable Monad

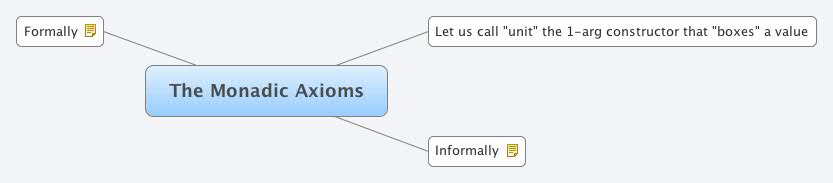
The Monadic Laws--Expressed informally:

1) If you unbox a value and box it again, you'll get "the same"** monad as the original.

2) If you map/flatmap a function f over a boxed value v, the result is "the same" as if you'd computed f(v) directly.

3) "Associativity" works. If you chain flatmap operations together, executing the flatmap operations in order is the same as flatmapping each individual element inside M with F and collecting the results.

** "The same" in a monadic context means that #equals and #hashCode say that the objects are the same, not necessarily that the values are literally the same reference or that they are internally implemented identically.

Formally

Formally:

1) m flatmap unit === m

2) unit(x) flatmap f === f(x) === x.f()

3) m flatmap g flatmap f === m flatmap {x => g(x) flatmap f }

(Remember: Unit is the generic name for a monad's 1-arg constructor)

Thanks to James Iry's blog series for this formulation of the Monad Laws.

Informally:

1) If you unbox a value and box it again, you'll get "the same" monad as the original.

2) If you map/flatmap a function f over a boxed value v, the result is "the same" as if you'd computed f(v) directly.

Why?

Because you might like to operate on boxed types without explicitly unboxing

Because you might like to transform the elements inside one box into different values stored in another box of the same type

Because you might like to copy the elements inside one box into another box of the same type

Because you'd like to preserve reasonable algebraic properties over those operations

Because it would be *really* nice if all of these operations could run in parallel, automatically

Java isn't able to do this...or is it?

The Trigram Problem

For example, given the input:

I wish I may I wish I might

You might generate:

"I wish" => ["I", "I"]

"wish I" => ["may", "might"]

"may I" => ["wish"]

"I may" => ["I"]

This says that the words "I wish" are twice followed by the word "I", the words "wish I" are followed once by "may" and once by "might" and so on.

To generate new text from this analysis, choose an arbitrary word pair as a starting point. Use these to look up a random next word (using the table above) and append this new word to the text so far.